Part 2: Capacitive Droppers.

Where the mains supply is AC, an elegant
idea is to use the reactance of a capacitor to drop the voltage. This resolves
the heat dissipation issue since capacitors do not (and should not) get
hot. In fact the scheme is also known as a "wattless dropper".
In the modern day, the scheme is popular
in some mains operated electronic devices such as time switches and PIR
sensors to obtain a low voltage DC supply. It is also very common with
LED bulbs operating from the mains supply.
It allows a much more compact construction
than if a transformer was used. It seems to be also becoming popular with
restorers of valve radios as a replacement for line cord resistors or other
troublesome resistive droppers. As we are dealing with a reactive component,
the frequency has to be taken into consideration, and of course the scheme
won't work on DC, since the capacitor presents an open circuit.
One would assume all that's necessary
to use a capacitor as a dropper is to work out its value so that the reactance
is the same as the resistance of a heater dropper that would otherwise
be used. However, there is a trap which many restorers are blissfully
unaware of, and which results in valve damage. Let's start with an important
formula:
Formula for capacitive reactance , Xc=
1/(2PI*F*C) where F is in c/s and C is in Farads. By transposing the
formula we can work out the capacitor value thus:
C= (1/Xc)/(2*PI*F)
For example, the capacitor value that would
be equivalent to 400 ohms with a 50c/s supply would be:
C=(1/400)/(2*3.14*50)
C= 7.96uF
The trap is the capacitor presents that
reactance only when there are no other components in the circuit. Once
a resistive component is introduced (e.g. a string of valve heaters), then
the current and voltage phase changes from 90 degrees, and it all becomes
more complex. The above formula is therefore not suitable. Without going
into phasor diagrams and other complexities, here is the correct way to
work out the required value. In this example, the heater string requires
84.8V at 600mA (it was actually a real situation with a TV set), and it
is to run from 240V 50c/s.
1. Work out the resistive value of the
load: R=84.8/.6
=141.3 ohms
2. Work out Z, where Z=Vsupply/load
current
=240/.6
= 400 ohms
3. Work out Xc by (Z^2-R^2)^.5
=(160,000 - 19965.7)^.5
= 374 ohms
4. Now work out C with the original
formula;
C=(1/374)/(2*3.14*50)
C= 8.5uF
This is the correct value of capacitance.
Now, what happens if one is unaware, and
assumes the capacitor is selected merely by reactance equivalent to when
a resistor is used? If the TV in the example used a resistive dropper,
the value would be: R=(240-84.8)/.6 which is 258 ohms. That's a big difference,
and if we select a capacitor with 258 ohms of reactance, the valves will
be very much over run! Incidentally, the capacitor value representing 258
ohms is: C=(1/258)/(2*3.14*50), or 12.3uF.
Other problems.
One may think all troubles are now over
having elegantly fitted the capacitor inside the midget set and done away
with the heat problems. Alas, there's more. First is the switch on surge.
A discharged capacitor presents a brief short circuit, and if the receiver
is turned on at the peak of the mains voltage, the heaters receive the
full mains voltage until the capacitor charges. The situation is worse
if the mains supply is momentarily interrupted while the capacitor is fully
charged, and the supply restored at the time when the sine wave is at the
opposite polarity to the charge in the capacitor. The two voltages then
add together. Such a situation might occur if the power switch is rapidly
flicked on and off, or the plug is not inserted fully into the power point.
The closer the sum of valve voltages is
to the supply, the less harm is likely, and in practice the capacitor charges
rapidly enough before the valve heaters have time to be overloaded. If
possible, it's a good idea to have some of the voltage dropped by a resistor
to reduce the surge current. (A surge resistor is essential when the dropper
feeds a rectifier for a low voltage DC supply, since the filter capacitor
will present a short circuit until it also charges).
Secondly, if the capacitor fails short
circuit, the heaters will receive the full mains voltage. Unfortunately,
in most instances, a fuse will not protect against this, because the difference
in current won't be enough to blow a fuse in time before the heaters are
damaged.
I designed a circuit which elegantly overcomes
this problem. It was used with an experimental three valve receiver:

Here we have a heater string requiring
18.9V at 600mA. As the valves used were not designed for series heater
use, there was a slight variation in heater current between valves. The
100R resistors are used to swamp out this difference. The 20R 20W resistor
reduces the switch on surge. It also isolates the Triac from switching
the capacitor directly - which will damage the Triac. The components of
interest are the back to back 30V zener diodes and the Triac. Basically,
the Triac is triggered should the voltage across it (and the heater chain)
rise above about 32Vpeak, or 22Vrms. This automatically prevents the heaters
being subjected to voltage surge. It also prevents damage should the capacitor
go short circuit. In this situation, the 20R will effectively be across
the mains and the fuse (not shown) will blow. Also, if one of the valve
heaters goes open circuit, the Triac triggers preventing the full mains
voltage appearing across the heater pins and burning out the associated
100R resistor. This circuit worked exceptionally well, and is highly recommended.
Even though it does use modern solid state parts, you can be assured the
valves are protected. I designed this circuit back in 1992, and improvements
I would make now would include a low value resistor to limit the Triac
gate current, and also a resistor between gate and earth to prevent false
triggering.
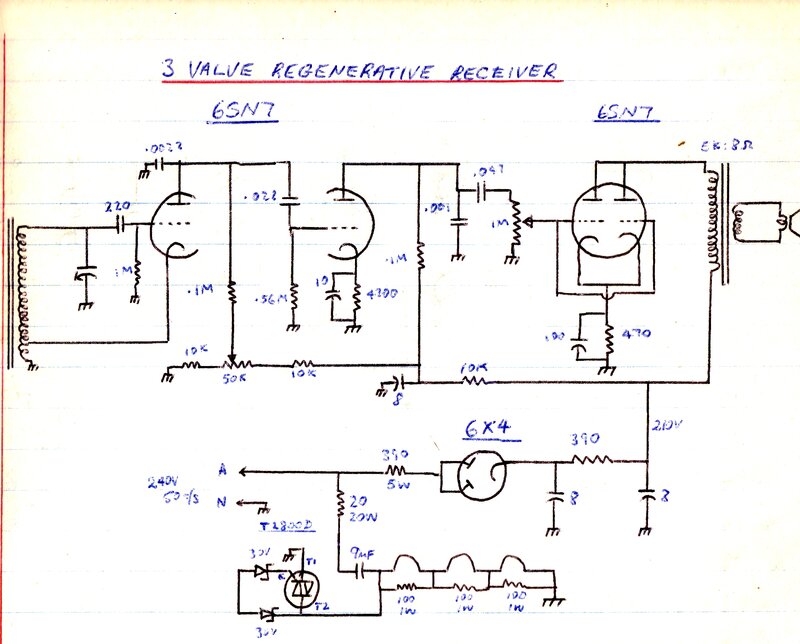
Full circuit of the receiver described above. Aerial coil was a
ferrite loopstick.
There are still limitations with capacitive
droppers. Next in line is that a capacitive dropper is frequency dependent.
If a circuit using a capacitive dropper is designed for 50c/s, but then
used on 60c/s, the valve heaters will be over run. In practice, this is
not usually a problem, since mains supplies in most areas are the one frequency
(one well known exception is Japan). The power factor is low, which
while not a problem with the reticulated mains supply, is not looked
upon favourably by the supply authorities.
Equipment fitted with capacitive droppers
are not suited for powering from inverters. Not only do inverters not like
the low power factor, but cheaper inverters output a square wave. The higher
frequency components of the square wave will cause a higher current to
flow through the capacitor. Simple inverters using radio type vibrators
output 100c/s. Again, the current flow will be excessive due to the square
wave, as well as the higher frequency. In essence, the inverter will be
damaged by the capacitive load. It, and the equipment will have a short
life.
Not Suitable for Inverters.
To illustrate why a capacitive dropper
designed for a sinusoidal mains supply is unsuitable with an inverter,
the following test setup was constructed. A 12V 5W light bulb was connected
in series with a 2.5uF capacitor, and connected to the 240V mains. Incidentally,
the power factor measured 0.012. This is far from the ideal 1, presented
by a purely resistive load.

Voltage across lamp with sinusoidal mains supply.
The voltage across the light bulb measured
3V. Next, the circuit was fed from a 240V 50c/s inverter which outputs
a square wave.

When fed from the inverter, the voltage across the bulb is more
than doubled.
Despite the inverter also producing a 240V
50c/s output, the voltage across the lamp was now 7.7V, which is more than
double what it was previously. The difference is the inverter puts out
a square wave, whereas the mains supply is sinusoidal.
Selecting the right type of capacitor.
If you've decided that the capacitive
dropper is the way to go, then you need to select the right capacitor type.
Do not use any kind of electrolytic! Even non polarised ones are not designed
for continuous AC across them. Neither are back to back polarised types.
You must use one that is rated for continuous operation across the AC mains.
Such examples are motor run, or phase correction capacitors as used with
fluorescent lights. Some motor start capacitors are non polarised electrolytics.
Do not use them, as they are for intermittent use only. Do not use DC capacitors.
A 400 or 630V DC capacitor is not suited for continuous AC mains operation.
Because of the odd value likely, you'll probably have to parallel smaller
capacitors to bring it up to value, or as I did above, introduce extra
resistance to reduce the voltage from a slightly larger capacitor. It
is essential that the heater voltages be checked once the circuit has been
brought into operation. Capacitor tolerances and other things can result
in non optimal voltages, and this needs to be corrected. Finally, if you
are concerned about shock hazard when the plug pins are touched after being
unplugged, connect a resistor across the capacitor to discharge it. Typical
values would be around 330K 1W. Too high and the capacitor takes too long
to discharge, and too low, it dissipates more power.
Commercially made examples:
HMV F33A Record Player.

For 226 to 250V, the dropper capacitor
is 4.4uF. For 220-225V, an extra 0.5uF is paralleled with that, bringing
the total capacitance to 4.9uF. As can be seen from the valve types, the
heater current is 300mA. Heater voltages add up to about 91V.
Thorn 1580 Television.

This British television design from the
early 1970's uses a 4.23uF capacitor to drop the voltage. Note the 470k
discharge resistor.
Let's reverse engineer this, and see if
our calculated capacitor matches that used by the manufacturer.
| Valve |
Heater Voltage |
| CRT |
6.3 |
| V1 ECC82 |
6.3 |
| V2 PCF80 |
9 |
| V3 PCL805 |
18 |
| V4 PL81 |
21.5 |
| V5 PY801 |
19 |
Total voltage = 80.1V @ 300mA
1. Work out resistive value of the load:
R = V / I.
= 80.1/0.3
= 267 ohms.
2. Work out Z = Vsupply / load current
= 240 / 0.3
= 800 ohms.
3. Work out Xc = (Z^2-R^2) ^0.5
= (800^2 - 267^2) ^0.5
= (640,000 - 71,289) ^0.5
= 754.1 ohms
4. Now work out C with the original
formula;
C = (1/754.1) / (2*3.14*50)
= 0.001326 / 314
= 4.22uF.
As can be seen, this is the correct way
to calculate the value for a capacitive dropper. The 0.01uF discrepency
is trivial, and would be likely to using less than the full amount of decimal
places in the above calculation.
There was a series of articles in Practical
Wireless describing capacitive droppers, ending in the design of a radio
receiver using one. The issues to look at are January, February, and March
of 1950.
Home








